Understanding Positive & Negative Numbers on the Number Line

Understanding the concept of positive and negative numbers on the number line is fundamental in mathematics. Whether you're a student, educator, or someone looking to refresh their math skills, grasping this basic idea is crucial. The number line serves as a visual tool to represent numbers, their relationships, and operations. By mastering positive and negative numbers, you'll be better equipped to tackle more complex mathematical problems, from basic arithmetic to advanced algebra. (number line basics, positive and negative numbers)
What is a Number Line?

A number line is a straight horizontal line with numbers placed at even intervals. It typically extends infinitely in both directions, representing all real numbers. The center point is zero, with positive numbers to the right and negative numbers to the left. This simple yet powerful tool helps in visualizing number comparisons, additions, subtractions, and more. (number line definition, real numbers)
Positive Numbers on the Number Line

Positive numbers are values greater than zero. On the number line, they are positioned to the right of zero. For example, 1, 2, 3, and so on are positive numbers. These numbers represent quantities, measurements, or values that are above zero. Understanding positive numbers is essential for basic counting, measurement, and arithmetic operations. (positive numbers, number line visualization)
Negative Numbers on the Number Line

Negative numbers are values less than zero. On the number line, they are positioned to the left of zero. Examples include -1, -2, -3, and so on. Negative numbers often represent deficits, debts, or temperatures below zero. Mastering negative numbers is crucial for understanding concepts like loss, decrease, and operations involving subtraction. (negative numbers, number line representation)
How to Work with Positive and Negative Numbers
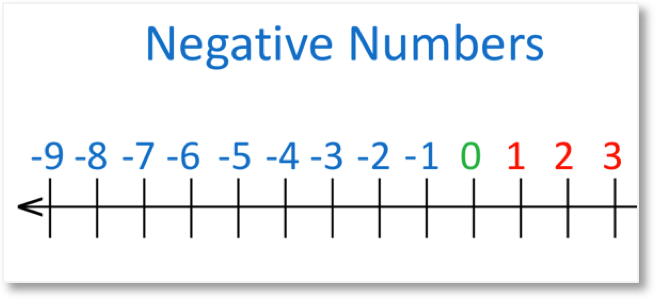
Adding and Subtracting on the Number Line
When adding or subtracting numbers on the number line, you move right for addition and left for subtraction. For example, to add 3 and -2, start at 3 and move 2 units to the left, landing on 1. This visual approach helps in understanding the flow of numbers and their operations. (number line operations, addition and subtraction)
| Operation | Example | Result |
|---|---|---|
| Addition | 3 + (-2) | 1 |
| Subtraction | 5 - 3 | 2 |

📌 Note: Always start at the first number and move according to the operation. For addition, move right; for subtraction, move left.
Comparing Numbers on the Number Line
Comparing numbers is straightforward on the number line. The number to the right is always greater than the number to the left. For instance, -3 is less than 2 because -3 is positioned to the left of 2. This visual comparison aids in understanding inequalities and number relationships. (number comparison, inequalities)
Practical Applications of Positive and Negative Numbers

Positive and negative numbers have real-world applications in various fields. For example, they are used in finance to represent profits and losses, in science to denote temperatures above and below zero, and in geography to indicate elevations. Understanding these concepts ensures accuracy in calculations and interpretations. (real-world applications, financial math)
- Use positive numbers for quantities greater than zero.
- Use negative numbers for quantities less than zero.
- Practice adding and subtracting on the number line.
- Compare numbers by their position on the number line.
In summary, the number line is an invaluable tool for understanding positive and negative numbers. By visualizing numbers and their operations, you can enhance your mathematical skills and apply them in practical scenarios. Whether you're solving basic problems or tackling complex equations, a solid grasp of the number line will serve as a strong foundation. (number line mastery, mathematical skills)
What is the purpose of a number line?
+A number line is used to visualize numbers, their relationships, and operations, making it easier to understand concepts like addition, subtraction, and comparison.
How do you represent negative numbers on a number line?
+Negative numbers are represented to the left of zero on the number line, indicating values less than zero.
Can you add a positive and a negative number on the number line?
+Yes, start at the positive number and move left by the absolute value of the negative number to find the result.



